V&V-Symbolic MC and Bounded MC

Symbolic Model Checking (SMC)

Nel model checking con formule LTL il procedimento, molto semplificato, consisteva in:

1. considerare una struttura di Kripke o un qualsiasi altro modello del nostro sistema
2. considerare una formula LTL
3. calcolare il behavior graph tramite il grafo delle computazioni del sistema e il tableau della formula LTL
4. cercare un sottografo adeguato

Ovviamente più variabili vengono usate nel sistema, più possibili configurazioni possono essere realizzate e di conseguenza il numero di stati del behaviour graph aumenta, rendendo più complicata la memorizzazione del modello e la ricerca del sottografo adeguato.

Il problema degli stati è anche chiamato state-space explosion problem.

I model checker con stati espliciti hanno un limite al numero di stati che riescono a gestire prima di essere eccessivamente costosi in termine spazio, ed è $10^6$.

Il symbolic model checking ha l’obiettivo di risolvere questo benedetto state-space explosion problem.

Ma come fa?

Cosa cambia nel Symbolic Model Checking

L’intuizione che hanno avuto è stata: perchè usare un modello che enumera tutte le possibili configurazioni? Non esiste un modo per rappresentare stati e transizioni in modo più compatto?

Ecco, i Symbolic Transition System (STS) sono proprio una rappresentazione compatta dei sistemi di transizione in cui si utilizzano espressioni simboliche per descrivere gli stati e le transizioni, invece di elencare esplicitamente tutti i possibili stati del sistema.

Formalmente, un STS è una quadrupla:

dove:

• S è l’insieme degli stati (descritti simbolicamente, ad esempio con variabili booleane).
• $I(x)$ è la condizione che definisce gli stati iniziali.
• $T(x,x′)$ è la relazione di transizione, che collega uno stato $x$ con il suo successore $x′$.
• $L$ è una funzione di etichettatura che associa a ogni stato le proprietà atomiche che sono vere in quello stato.

Una traccia (path) è una sequenza infinita di assegnamenti ai valori delle variabili di stato, tale che:

• $m_0\vDash I(x)$, ossia il primo stato soddisfa la condizione iniziale.
• $\forall i\ge 0$ la coppia $(m_i,m_{i+1})$ soddisfa la relazione di transizione $T(x,x′)$ (in poche parole due stati sono successivi se esiste una transizione che passa da un certo assegnamento delle variabili x, a un altro x’).

In pratica, invece di considerare direttamente un enorme grafo di stati, lavoriamo su una rappresentazione più compatta che esprime in modo simbolico come gli stati si evolvono nel tempo

Ci sono 3 tecniche di symbolic model checking:

• partial order reduction
• BDD-based symbolic model checking
• SAT-based symbolic model checking, aka Bounded Model Checking.

Ordered Binary Decision Diagrams(OBDD)

Gli Ordered Binary Decision Diagrams (OBDD) sono una tecnica utilizzata nel contesto del Symbolic Model Checking per mitigare lo State Explosion Problem.

A differenza degli approcci espliciti, il Symbolic Model Checking utilizza rappresentazioni compatte basate su formule booleane, evitando di enumerare esplicitamente tutti gli stati. Gli OBDD sono una delle principali strutture dati utilizzate in questo contesto, poiché permettono di rappresentare e manipolare insiemi di stati e transizioni in modo compatto ed efficiente.

Gli OBDD differiscono rispetto ai classici alberi di decisione (decision trees) perché applicano tecniche di riduzione per eliminare variabili non influenti o ridondanti. In particolare:

• Eliminano sottoalberi isomorfi, unificando sotto-espressioni identiche per ridurre la ridondanza.
• Rimuovono nodi inutili, come quelli che non influenzano il risultato finale della funzione booleana rappresentata.

Nell’immagine si può vedere un esempio di riduzione di un BDT in un OBDD

Nel Symbolic Model Checking, gli OBDD vengono utilizzati per rappresentare l’insieme degli stati e delle transizioni del sistema in modo compatto, consentendo di eseguire operazioni come il calcolo dei predecessori o dei punti fissi senza dover esplorare esplicitamente l’intero spazio degli stati. Questo approccio ha permesso la verifica di sistemi molto più grandi rispetto ai metodi classici basati su enumerazione esplicita degli stati.

1. Cosa rappresenta un OBDD?

Un OBDD è una rappresentazione compatta e ordinata di una funzione booleana. Invece di elencare esplicitamente tutte le assegnazioni di verità (come in una tabella di verità), l’OBDD utilizza una struttura ad albero per rappresentare la funzione in modo efficiente, sfruttando ridondanze e ordinando le variabili in modo ottimale.

• Le variabili di stato di un sistema sono rappresentate come variabili booleane.
• Le transizioni del sistema sono descritte con formule booleane che coinvolgono queste variabili.
• L’OBDD permette di comprimere queste formule, eliminando ridondanze e ottimizzando l’uso della memoria.

Esempio:
Supponiamo che il tuo sistema abbia due variabili di stato $x_1$ e $x_2$. Invece di memorizzare esplicitamente tutte le possibili transizioni (ad esempio, $(x_1, x_2) \rightarrow (x_1’, x_2’)$), l’OBDD rappresenta l’intera relazione di transizione come una funzione booleana compatta, riducendo notevolmente la complessità spaziale.

2. Uso dell’OBDD nel Model Checking

Una volta costruito l’OBDD del sistema, il model checking simbolico opera direttamente su di esso. Ecco come funziona:

1. Codifica delle transizioni
   • L’insieme degli stati è rappresentato da una funzione booleana $S(x)$, dove $x$ è un vettore di variabili di stato.
   • La relazione di transizione è codificata come una funzione $T(x, x’)$, che descrive come le variabili di stato attuali ($x$) si trasformano nelle variabili di stato future ($x’$).
2. Verifica delle proprietà (CTL Model Checking)
   • Le formule logiche CTL (Computational Tree Logic) vengono tradotte in operazioni sui BDD.
   • Per ogni formula $\varphi$, il model checker costruisce un OBDD che rappresenta l’insieme degli stati che soddisfano $\varphi$.
   • Le operazioni logiche come $\land$ (AND), $\lor$ (OR) e $\neg$ (NOT) vengono eseguite direttamente sui BDD, sfruttando la loro struttura compatta per garantire efficienza.
3. Calcolo degli insiemi di stati raggiungibili
   • Utilizzando l’OBDD, è possibile calcolare l’insieme degli stati raggiungibili a partire da uno stato iniziale, applicando iterativamente la relazione di transizione $T(x, x’)$.
   • Questo processo è alla base della verifica di proprietà di raggiungibilità e sicurezza.
4. Verifica di proprietà temporali
   • Per verificare proprietà temporali come $\text{AG } \varphi$ (tutti gli stati raggiungibili soddisfano $\varphi$) o $\text{EF } \varphi$ (esiste uno stato raggiungibile che soddisfa $\varphi$), il model checker utilizza algoritmi basati su operazioni di punto fisso (fixed-point) sui BDD.

3. Vantaggi degli OBDD nel Model Checking

• Efficienza: Gli OBDD permettono di rappresentare funzioni booleane complesse in modo compatto, riducendo il consumo di memoria e migliorando le prestazioni.
• Flessibilità: Le operazioni logiche sui BDD sono ben definite e possono essere combinate per verificare proprietà complesse.
• Scalabilità: Grazie alla loro struttura, gli OBDD sono adatti per sistemi con un numero elevato di variabili di stato, purché le funzioni booleane abbiano sufficiente regolarità.

4. Esempio Pratico

Supponiamo di avere un sistema con due variabili di stato $x_1$ e $x_2$, e una relazione di transizione descritta dalla formula: \(T(x_1, x_2, x_1', x_2') = (x_1' = x_1 \land x_2) \lor (x_2' = \neg x_1)\) Un OBDD può rappresentare questa relazione in modo compatto, evitando di enumerare tutte le possibili combinazioni di $x_1, x_2, x_1’, x_2’$.

1. Costruzione Bottom-Up della Funzione di Transizione

Se hai già una funzione di transizione espressa in termini di operazioni booleane (ad esempio, $x_1’ = x_1 \oplus x_2$, $x_2’ = x_2 \land x_3$, ecc.), puoi costruire l’OBDD in modo bottom-up:

1. Parti dalle foglie: Le foglie rappresentano i valori $0$ e $1$.
2. Costruisci i sotto-OBDD: Per ogni operazione booleana (ad esempio, $\oplus$, $\land$, $\neg$), costruisci ricorsivamente i sotto-OBDD delle sotto-formule.
3. Combina i sotto-OBDD: Applica le operazioni booleane ai sotto-OBDD per ottenere l’OBDD completo della funzione di transizione.
4. Riduci l’OBDD: Elimina i nodi ridondanti per compattare la rappresentazione.

Esempio:
Se la funzione di transizione è:

costruisci prima l’OBDD per $x_1 \land x_2$, poi per $\neg x_2$, e infine combinali con un’operazione AND.

2. Costruzione Top-Down della Formula di Transizione

Se hai già un OBDD e vuoi ricavare la formula di transizione corrispondente, puoi operare in modo top-down:

1. Parti dalla radice: La radice rappresenta una delle variabili (ad esempio, $x_1$).
2. Segui i rami: Per ogni nodo, segui i rami $0$ e $1$ (che corrispondono ai valori della variabile).
3. Imponi i vincoli: Man mano che scendi nell’albero, imponi i vincoli sulle variabili in base ai valori dei nodi figli.
4. Ricostruisci la formula: Combinando i vincoli lungo i percorsi che portano al valore $1$ (vero), ottieni la formula di transizione.

Esempio:
Supponiamo di avere un OBDD con radice $x_1$, dove:

• Se $x_1 = 0$, il ramo porta a un nodo $x_2$.
• Se $x_1 = 1$, il ramo porta direttamente a $0$.
• Se $x_2 = 0$, il ramo porta a $1$.
• Se $x_2 = 1$, il ramo porta a $0$.

La formula di transizione corrispondente è:

Perché solo il percorso $x_1 = 0$ e $x_2 = 0$ porta a $1$.

Confronto tra i Due Approcci

• Bottom-Up: È utile quando hai una funzione di transizione già definita e vuoi costruire l’OBDD corrispondente. È un approccio costruttivo.
• Top-Down: È utile quando hai un OBDD e vuoi ricavare la formula di transizione che rappresenta. È un approccio analitico.

Cose utili per manipolare OBDD

Ora spiegherò 3 cose utili da sapere se si vuole giocare con gli OBDD. Ovviamente quello che sto per mostrare è la notazione formale per svolgere certe operazioni, ma l’idea intuitiva è abbastanza banale. All’inizio non capivo perchè le dovessimo formalizzare in questa maniera, ma poi ho capito che è solo perchè di base gli OBDD sono una struttura dati, quindi nella pratica saranno codificati in maniera complicata, oppure avremo solo la formula logica che rappresenta la funzione booleana che gioca con gli assegnamenti delle variabili. Le operazioni utili che mostrerò sono:

• funzione restrict
• espansione di Shannon
• combinazione di OBDD

1. Funzione Restrict

La funzione restrict viene utilizzata per forzare una variabile booleana ( x_i ) a essere costante, ossia ad assumere sempre il valore 0 o 1. Formalmente, si scrive:

Questo significa che, invece di considerare $x_i$ come una variabile che può assumere entrambi i valori 0 e 1, la fissiamo al valore ( b ) (che può essere 0 o 1) e analizziamo la funzione booleana risultante.

🔹 Esempio pratico:

Supponiamo di avere la funzione booleana:

Se applichiamo il restrict con $x_1 = 1$, otteniamo:

Se applichiamo il restrict con $x_1 = 0$, otteniamo:

📌 Applicazione agli OBDD:
Nei diagrammi OBDD, quando un nodo rappresenta la variabile $x_i$, viene rimpiazzato con il suo figlio low (se $b = 0$) o con il suo figlio high (se $b = 1$). Questo riduce la dimensione dell’OBDD eliminando rami inutili.

2. Espansione di Shannon

L’espansione di Shannon è una tecnica che permette di scomporre una funzione booleana in termini delle sue variabili, dividendo la funzione in due parti:

• una in cui la variabile ( x ) è 0,
• una in cui la variabile ( x ) è 1.

La formula è:

🔹 Esempio pratico:
Consideriamo la funzione booleana:

Se usiamo l’espansione di Shannon su $x_1$, otteniamo:

Quindi possiamo scrivere:

📌 Applicazione agli OBDD:
Questa formula è il fondamento della costruzione degli OBDD, perché permette di decomporre una funzione booleana ricorsivamente, creando una rappresentazione compatta dell’insieme delle assegnazioni.

3. Combinazione di due OBDD

Se vogliamo rappresentare un’operazione booleana $*$ tra due funzioni$f$ e $f’$ tramite OBDD, dobbiamo combinare i loro grafi. Il metodo segue queste regole:

• Se i due nodi sono terminali (foglie), allora l’operazione si applica direttamente ai valori.
  🔹 Esempio: $ 1 \land 0 = 0 $

• Se entrambi i nodi rappresentano la stessa variabile $x$, applichiamo l’espansione di Shannon e risolviamo i due rami separatamente.

• Se il nodo di $f$ ha una variabile $x$ minore rispetto a quella del nodo di $f’$, significa che dobbiamo espandere solo $x$ (e viceversa se è maggiore).

• Ogni sottoproblema creato è una coppia di sottografi, e il numero massimo di questi sottoproblemi è limitato dal prodotto cartesiano tra gli OBDD delle due funzioni.

📌 Conseguenza:
Nonostante gli OBDD riducano la complessità rispetto alla rappresentazione esplicita degli stati, il numero massimo di nodi dell’OBDD risultante può ancora essere esponenziale nel peggiore dei casi, anche se nella pratica è molto più gestibile.

4. OBDD per la Negazione

Un’operazione molto semplice sugli OBDD è la negazione di una funzione booleana $f$, che viene ottenuta semplicemente scambiando i nodi terminali:

• Se un nodo foglia contiene 0, lo trasformiamo in 1.
• Se un nodo foglia contiene 1, lo trasformiamo in 0.

🔹 Esempio pratico:
Se l’OBDD di una funzione booleana ha una foglia 1 in un certo ramo, il suo complementare avrà 0 nello stesso ramo e viceversa.

Riassunto

1. Restrict: fissa una variabile a 0 o 1, semplificando l’OBDD.
2. Espansione di Shannon: scompone una funzione booleana in due casi (quando la variabile è 0 o 1), ed è il principio base per la costruzione degli OBDD.
3. Combinazione di due OBDD: applica operazioni booleane ($\lor, \land, \oplus$) combinando le strutture con l’espansione di Shannon.
4. Negazione di un OBDD: scambia i valori dei nodi terminali 0 e 1.

Bounded Model Checking (BMC)

(SAT solvers + symbolic model checking +bounded models) Il bounded model checking è una tecnica usata per eseguire il model checking LTL vincolando la dimensione della computazione da considerare. Praticamente invece di vedere all’intera sequenza infinita di passi (che diventa complicato e potenzialmente molto costoso) ci concentriamo solo su una porzione.

Analizziamo come potrebbe essere fatta la computazione di un sistema:

1. potrebbe avere un ciclo,

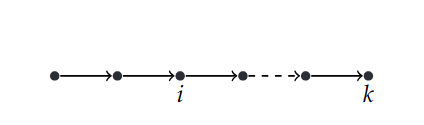
1. oppure potrebbe non avere nessun ciclo

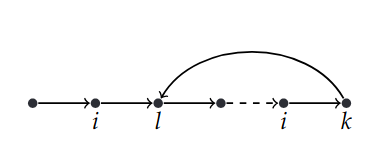
1. potrebbe non avere cicli nei primi $z$ stati e un ciclo che inizia dallo stato $s_i$ e termina nello stato $s_j$.

Nel primo caso per poter stabilire se una formula LTL è sempre valida all’interno del sistema non serve analizzare una sequenza infinita, ma mi basta controllare se la formula è vera all’interno del percorso finito in cui avviene il loop.

Se la computazione è del tipo A,B,C,D, A,B,C,D, …, ovviamente la proprietà di “non compare mai E” deve valere all’interno del ciclo A,B,C,D

Nel secondo caso invece il model checking bounded mi permette di verificare che per almeno $k$ steps la formula LTL da verificare sia soddisfatta da qualsiasi computazione.

Ma come fa? Controlla tutte le computazioni possibili?

Bè, no. In realtà trasforma il problema di universalità $\mathcal{M},s \vDash A\psi$ in un problema di esistenzialità, ossia si controlla se $\mathcal{M},s \vDash E \lnot \psi$.

A quel punto è sufficiente controllare se esiste una computazione $\pi$ di $\mathcal{M}$ tale che soddisfa la regola $\varphi = \lnot\psi$.

Per farlo codifichiamo il problema $\mathcal{M}$ in SAT e lanciamo un SAT-solver su $(\mathcal{M}, \varphi)$. Se il solver trova una computazione che funziona significa che esiste una computazione che viola il programma $\mathcal{M}$.

Ovviamente tutto questo è: BOUNDED. Quindi ci tocca considerare delle computazioni di lunghezza finita.

Semantica per il bounded model checking in LTL

È chiaro che non possiamo usare la semantica LTL che abbiamo usato in precedenza, perchè era studiata per ragionare su computazioni infinitamente lunghe, non limitate.

Quindi semplicemente riprendiamo le formule che avevamo visto per LTL classico, ossia

$M,x^i \vDash P \iff P \in L(s_i)$

$M,x^i \vDash p \land q \iff (M,x^i \vDash p) \land (M,x^i \vDash q) $

$M,x^i \vDash p \lor q \iff (M,x^i \vDash p) \lor (M,x^i \vDash q) $

$M,x^i \vDash \lnot p \iff M,x^i \not \vDash p $

$M,x^i \vDash p U q\iff \exists j \ge i (M,x^j \vDash q) \land \forall i \le k \le j(M,x^i \vDash p)$

$M,x^i \vDash Xp \iff M,x^{i+1} \vDash p$

e le modifichiamo affinchè $\pi \vDash_k^i \varphi$ se e solo se:

$\pi \vDash_k^i p \iff p \in L(\pi_i)$

$\pi \vDash_k^i \lnot p \iff p \not \in L(\pi_i)$

$\pi \vDash_k^i p \land q \iff (\pi \vDash_k^i p) \land (\pi \vDash_k^i q) $

$\pi \vDash_k^i p \lor q \iff (\pi \vDash_k^i p) \lor (\pi \vDash_k^i q) $

$\pi \vDash_k^i p U q\iff \exists k\ge j \ge i (\pi \vDash_k^j q) \land \forall i \le h \le j(\pi \vDash_k^h p)$

$\pi \vDash_k^i Xp \iff i\le k \land \pi \vDash_k^{i+1} p$

Da un problema di BMC a un problema SAT

L’obiettivo è quello di capire se una certa traccia soddisfa o meno una certa proprietà \psi$. Perciò il problema in realtà è di soddisfacibilità, quindi ha senso convertire il problema $\pi \vDash_k^i \varphi$ in un problema SAT.

L’idea è quindi di convertire $\pi$ e $\varphi$ in una formula logica del tipo $\llbracket M, \varphi \rrbracket_k$ dove:

Traduzione del modello $M$

Dove:

• $I(s_0)$ rappresenta lo stato iniziale.
• $T(s_i,s_{i+1})$ rappresenta la relazione di transizione tra gli stati $s_i​$ e $s_{i+1}$.

Riconoscimento del loop

Traduzione $\varphi$

$ _l\llbracket p \rrbracket_k^i = p(s_i)$

$ _l\llbracket \lnot p \rrbracket_k^i = \lnot p(s_i)$

$ _l\llbracket \varphi_1 \land \varphi_2 \rrbracket_k^i = \;\ _l\llbracket \varphi_1 \rrbracket_k^i \land \; \ _l\llbracket \varphi_2 \rrbracket_k^i$

$ _l\llbracket \varphi_1 \lor \varphi_2 \rrbracket_k^i = \;\ _l\llbracket \varphi_1 \rrbracket_k^i \lor \; \ _l\llbracket \varphi_2 \rrbracket_k^i$

$ _l\llbracket X\varphi \rrbracket_k^i = \;\ _{l}\llbracket \varphi \rrbracket_k^{\;(i \mod k)} $

$ _l\llbracket G\varphi \rrbracket_k^i = \;\ _l \llbracket \varphi \rrbracket_k^i \land \; \ _{l}\llbracket G\varphi \rrbracket_k^{\;(i+1 \mod k)} $

$ _l\llbracket F\varphi \rrbracket_k^i = \;\ _l \llbracket \varphi \rrbracket_k^i \land \; \ _{l}\llbracket F\varphi \rrbracket_k^{\;(i+1 \mod k)} $

$ _l\llbracket \varphi_1 U \varphi_2 \rrbracket_k^i = \;\ _{l}\llbracket \varphi_1 \rrbracket_k^{\;(i \mod k)} \lor (\;\ _{l}\llbracket \varphi_1 \rrbracket_k^{\;i} \land \; \ _l\llbracket \varphi_1 U \varphi_2 \rrbracket_k^{(i+1 \mod k)})$

Formula finale

dove:

• $\llbracket M \rrbracket_k^i$ rappresenta il sistema fino a $k$
• $\lnot L_k \land \llbracket \varphi \rrbracket_k^0$ serve a controllare la parte senza loop
• $\bigvee_l \ _lL_k \land \ _l\llbracket \varphi \rrbracket_k^0$ serve a controllare i loop

Verificare la soddisfacibilità della formula

Per verificare se la formula ammette effettivamente delle soluzioni (e quindi se esiste una computazione che soddisfa la suddetta formula LTL) è sufficiente assumere $\llbracket M \rrbracket_k = true$ e lanciare un sat solver solo sulla parte restante della formula.

Se il SAT solver restituisce SAT significa che esiste una computazione che soddisfa la formula.

Domande che mi sono posto

1. Ma quindi OBDD è solo una tecnica per creare una rappresentazione compatta di stati e funzione di transizione, ma da sola non permette di eseguire un model checking? C’è comunque bisogno di un modello come le Kripke structures? Essenzialmente è così.

2. Qual è la funzione delle operazioni restrict, shannon expansion, negazione di OBDD e combinazione di OBDDs?

3. Qual è la differenza sostanziale tra OBDD e Bounded Model checking?

4. Ma quindi posso usare il bounded model checking aggiungendo come layer iniziale un bell’OBDD per usare una rappresentazione compatta?