V&V-Model Checking
Model checking nella logica temporale
Quando parliamo di model checking nella logica temporale intendiamo quel processo in cui andiamo a verificare che un certo sistema garantisca determinate proprietà. Ad esempio in un sistema operativo attraverso il model checking possiamo verificare la capacità dello stesso di evitare situazioni di deadlock o di starvation.
Chiaramente poter verificare se un sistema garantisce o meno certe proprietà è fondamentale, basti pensare a quanto sia importante assicurare che la centralina di un veicolo garantisca l’attivazione dell’ABS in caso di pattinamento in frenata. Non è ammissibile mettere in commercio un dispositivo ABS che non garantisce la sua puntualità e disponibilità in ogni istante di tempo e computazione della centralina!
Ecco quindi che facciamo un passo in avanti rispetto alle semplici definizioni di formule LTL e CTL, introducendo un metodo per legarle a una specifica computazione o a un insieme di possibili computazioni.
Model checking per LTL
Il model checking per una formula LTL corrisponde al verificare la P-satisfiability di un programma, ossia se un certo programma ammette una soluzione.
Dove vogliamo arrivare:
Se $B_{(P,\varphi)}$ contiene una componente adeguata allora la formula è soddisfabibile.
1. Definizioni di base
Diamo ora alcune definizioni di base:
| concetto | definizione |
|---|---|
| state(A) | corrisponde alla congiunzione delle formule locali di un atomo A |
| consistenza | data una computazione $\Theta = s_0,s_1,s_2, \dots$ e un cammino $\sigma$ del tableau di $\varphi$, diciamo che lo stato $s_i$ è consistente rispetto all’atomo $A_i$ se $s_i \vDash State(A_i)$ |
| trail | data una computazione $\sigma = s_0,s_1,s_2, \dots$ e un cammino $\Theta$ del tableau di $\varphi$, diciamo che $\Theta$ è una trail per $\sigma$ se $\forall i \ge 0$ abbiamo che $s_i$ è consistente rispetto all’atomo $A_i$ |
Behavior Graph
A partire dal tableau $T_\varphi$ di una formula LTL $\varphi$ e dal grafo delle computazioni $G_P$ di un programma $P$, è possibile costruire il behavior graph, che altro non è che la fusione dei due.
Consideriamo il seguente grafo delle computazioni
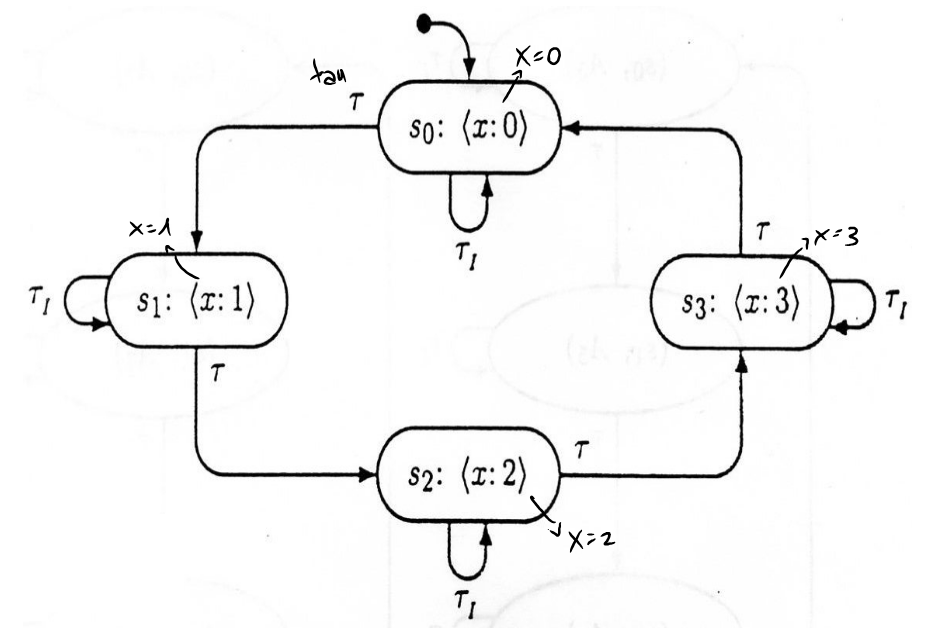 e il tableau
e il tableau
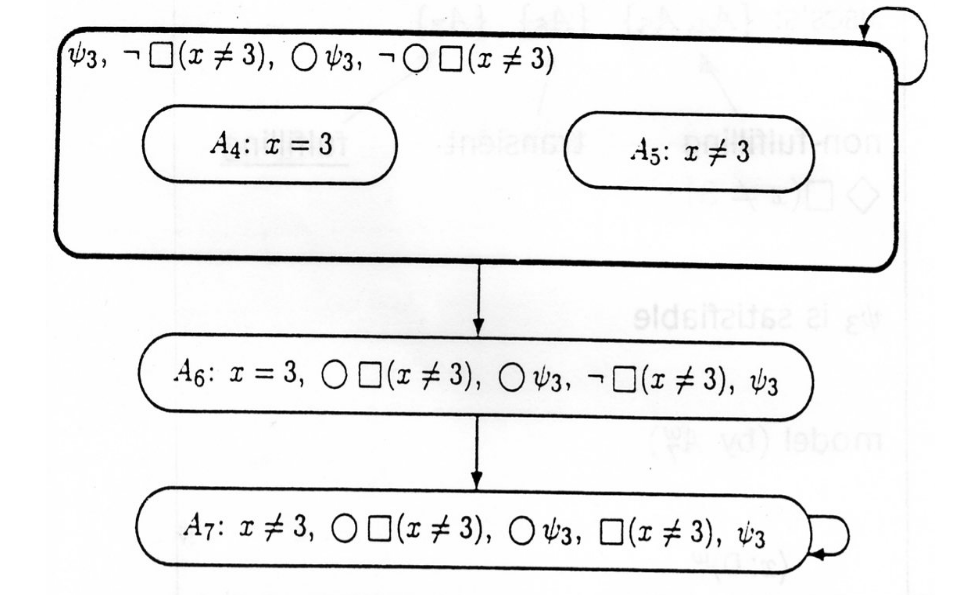 Semplicemente seguendo questo schema:
Semplicemente seguendo questo schema:
- considero tutti gli stati così formati
- prendo un atomo $A$ di $T_\varphi$
- prendo un stato $s$ del grafo delle computazioni $G_P$
- controllo se $s$ è consistent rispetto a $A$
- se lo è allora creo un nodo $(s,A)$
- se non lo è considero riprendo dal punto 2
- considero ogni stato che ho ottenuto dal punto 1 e congiungo tutte le coppie di stati del tipo $(s_i, A_i)$ e $(s_j, A_j)$ in cui $s_i$ è un successore di $s_j$ nel grafo $G_P$ e $A_i$ è un successore di $A_j$ nel tableau $T_\varphi$.
Un esempio di risultato finale è il seguente:

Ottenuto questo benedetto Behavior Graph, diciamo che:
- lo stato $(s’,A’)$ è $\tau$-successore dello stato $(s,A)$ se esiste una transizione da $(s,A)$ a $(s’,A’)$
- una transizione è abilitata su $(s,A)$ se è abilitata su $s$
- una transizione $\tau$ è taken se esiste almeno un nodo $(s,A)$ per il quale $(s’,A’)$ è un suo $\tau$-successore
A questo punto dato un qualsiasi sottografo $S \subseteq \mathcal{B}_{P,\varphi}$ sappiamo che:
- S è just se ogni transizione in $\mathcal{J}$ è taken o disabilitata in qualche nodo
- S è compassionate se ogni transizione in $\mathcal{C}$ è taken o disabilitata in ogni nodo
- S è fair se è compassionate e just
- S è fulfilling se ogni nodo promettente è realizzato
- S è adeguato se S è fair e fulfilling
Ora, come dicevamo all’inizio, se $\mathcal{B}_{P,\varphi}$ contiene un sottografo adeguato, significa che esiste una computazione del modello che garantisce le proprietà della formula $\varphi$.
Ma perchè?
Bè, se un sottografo è adeguato significa che abbiamo:
- fulfillingness => quindi la formula LTL è soddisfacibile (l’avevamo visto quando abbiamo parlato di LTL satisfiability)
- fairness => quindi le transizioni soddisfano le proprietà di justice e compassion
👁️ Attenzione, la componente adeguata è sufficiente a dimostrare la soddisfacibilità della formula sul modello, non la sua validità! Per verificare la validità è necessario negare la formula e dimostrare che è insoddisfacibile.
2. Procedimento
L’idea è questa:
- Costruisco il grafo delle computazioni $G_P$ per il programma P
- Costruisco il tableau $T_\varphi$ per la formula LTL $\varphi$
- A partire da $G_P$ e $T_\varphi$ costruisco il behavior graph $B_{(P, \varphi)}$
- Decompongo $B_{(P,\varphi)}$ nei suoi MSCS $S_1, S_2, \dots, S_n$
- richiamo la procedura ADEQUATE_SUB per ogni sottografo di $B_{(P,\varphi)}$
- La procedura termina con $S’ \subseteq S$ e:
- se $S’ = \emptyset$ allora non esiste nessun sottografo adeguato e quindi il programma non soddisfa in nessun caso la formula LTL $\varphi$
- se $S’ \ne \emptyset$ allora $S’$ rappresenta proprio la componente adeguata che garantisce che esiste una computazione di P che soddisfa la formula LTL $\varphi$
La definizione di ADEQUATE_SUB è la seguente:
def Adequate_Sub(S:MSCS)->SCS:
if S.isNoTFulfilling():
return null #se non è fulfilling non ci interessa
if S.isNotJust():
return null #se non è just non ci interessa
#se è compassionate e ha superato i controlli precedenti significa che ho trovato la mia componente adeguata
if S.isCompassionate():
return S
# S è fulfilling e just ma non compassionate
# Identifichiamo il sottoinsieme T delle transizioni compassionate non prese in S
T = {t | t transizione and t abilitato in P and t non preso in S}
# Rimuoviamo EN(T, S) da S per ottenere U
U = S - EN(T,S)
#applico la procedura ricorsivamente su tutti i sottografi del sottografo
for new_S in getStronglyConnectedSubgraphs(U):
return Adequate_Sub(new_S)
Questo metodo permette di dimostrare la P-satisfiability, ovviamente per verificare la P-validity è sufficiente negare la formula LTL $\varphi$ e verificare la presenza di una componente adeguata per $B_{(P, \lnot \varphi)}$
3. Risultati
Ovviamente se $S’$ è un sottografo adequate, non è detto che S tale che $S’ \subset S$ sia anch’esso adequate. Questo è dato dal fatto che se S’ per essere adequate dev’essere fair e fulfilling, quindi just, compassionate e fulfilling, ma:
- se S’ è just allora S è just
- se S’ è fulfilling allora S è fulfilling
- se S’ è compassionate NON è detto che S sia compassionate
Model checking per CTL
Ecco, per CTL le cose cambiano un po’, perchè gli operatori di percorso aiutano a semplificare le cose.
Prima di spiegare bene le cose, è doveroso ricordare qual è la differenza tra LTL e CTL:
- LTL permette di esprimere vincoli sull’ordine globale degli eventi in una singola computazione
- MA NON VINCOLI DI POSSIBILITÀ
Ad esempio sarò in grado di definire la proprietà
Il forno non deve mai iniziare a scaldare prima che il pulsante di avvio sia stato premuto almeno una voltama non
Ogni volta che si preme il pulsante di avvio, esiste almeno un futuro in cui il forno si riscalderà - CTL permette di esprimere proprietà sulla struttura del modello
- MA NON VINCOLI DI FAIRNESS
Quindi ad esempio sarò in grado di definire la proprietà
È sempre possibile raggiungere uno stato in cui il forno si sta riscaldandoma non
Se l'errore accade, allora in questa computazione il forno non si scalderà mai più
Microwave example
Prendiamo come esempio le seguenti specifiche per il funzionamento di un forno a microonde:
To cook food in the oven, open the door, put the food inside,
and close the door. Do not put metal containers in the oven.
Press the start button. The oven will warmup for 30 seconds,
and then it will start cooking. When the cooking is done, the
oven will stop. The oven will stop also whenever the door is
opened during cooking. If the oven is started while the door is
open, an error will occur, and the oven will not heat. In such a
case, the reset button may be used
Un modello di Kripke che rappresenta il seguente sistema potrebbe essere qualcosa del genere

È evidente che le formule CTL che definiscono le proprietà per un modello corretto sono
- If the oven heats, then the door is closed:
- Whenever the start button is pushed, eventually the oven will heat:
- Whenever the oven is correctly started, eventually the oven will heat:
- Whenever an error occur, it will be still possible to cook:
Possiamo notare come il modello proposto non garantisca tutte le formule richieste affinchè un microonde rispetti le specifiche.
In particolare è facile osservare che la proprietà numero 2 è violata in questo punto

Si può vedere in modo analogo come anche le proprietà 3 e 4 non sono rispettate da questo modello.
Quello che sto per dire è molto importante per capire la differenza sostanziale tra LTL-MC e CTL-MC:
in CTL-MC non ci interessa osservare una computazione infinita, ma solo la struttura del modello per poter dire se una proprietà è violata o meno.
Algoritmo
Per il CTL-MC si applica il seguente algoritmo:
- si considera un modello di Kripke $M$ e una formula CTL $\alpha$ che il modello deve rispettare
- per ogni sottoformula $\beta$ di $\alpha$ si guarda se $\beta$ è del tipo AX $\gamma$ , EX $\gamma$, EU $\gamma$, AU $\gamma$
- se è EX $\gamma$: per ogni nodo del modello M, ne considero uno $m$
- verifico se esiste un nodo $v$ che è in relazione con $m$ (Rmv significa che c’è un arco che da $m$ va in $v$)
- se esiste allora controllo che la proprietà $\gamma$ appartenga all’insieme delle proprietà valide su $v$ (nello pseudocodice è quel $v\in V(v)$):
- se la proprietà si trova in $v$ allora aggiungo la CTL-formula $\beta$ alle proprietà del nodo $m$ (nello pseudocodice ${\beta} \cup V(m)$)
Procedo in modo analogo anche negli altri casi. Per l’operatore Until uso una procedura ricorsiva che non fa altro che eseguire per ogni nodo una procedura che ricerca quali nodi sono in relazione di transizione con il nodo considerato (per poi applicare la procedura in modo ricorsivo sui nodi trovati, finchè non si raggiunge il punto in cui non ci sono nodi di partenza o nodi non conosciuti).
Per chiarezza espositiva inserisco di seguito l’algoritmo sotto forma di pseudo-codice,



Model checking LTL vs CTL
Un’importante osservazione da fare è che il model checking di CTL è più rapido del model checking con formule LTL.
LTL-MC é PSPACE mentre CTL-MC è polinomiale rispetto alla dimensione del modello.
La differenza sta nel fatto che per CTL le proprietà possono essere verificate sugli stati singoli, propagando l’informazione localmente (ricordati dell’esempio del forno a microonde).
Per LTL invece certe proprietà possono dipendere da una serire infinita di scelte. Anche per questo motivo avremo bisogno di applicare il Bounded Model Checking nel caso LTL, perchè a volte il numero di stati “esplodeva” nel momento in cui generavamo il behaviour graph.
