V&V-Learning Automata

12 Feb 2025

Learning Automata: Imparare Automata a Stati Finiti e $\omega$-Automata

Gli automi sono modelli computazionali che riconoscono linguaggi (insiemi di parole) e, in particolare, i linguaggi regolari (per parole finite) o gli ω-linguaggi regolari (per parole infinite). Un aspetto fondamentale nella teoria degli automi è la possibilità di apprendere (o “learning”) l’automa corretto che riconosca un dato linguaggio, partendo da informazioni limitate e facendo interagire un learner (studente) e un teacher (insegnante) esperto del linguaggio target.

Quindi la prima cosa fondamentale da ricordare quando si parla di Learning Automata è che: esiste un learner ed esiste un teacher che interagiscono tra loro.

Il Modello di Apprendimento

Nel contesto del learning degli automi, il teacher conosce il linguaggio target $\mathcal{L}$ (che può essere, ad esempio, un linguaggio regolare o $\omega$-regolare) mentre il learner inizia conoscendo solo l'alfabeto di base e deve costruire progressivamente una ipotesi $\mathcal{A}$ (un automa, che si tratti di un DFA per linguaggi finiti o di un automa di Büchi, Müller o Rabin per $\omega$-linguaggi).

Il modello di apprendimento tipico si basa su due tipi di query:

Membership Query (MQ): Il learner propone una parola $w$ e chiede al teacher: “È $w$ appartenente al linguaggio $\mathcal{L}$?” Il teacher risponde “sì” o “no”.

Equivalence Query (EQ): Il learner propone l’automa $\mathcal{A}$ (o, equivalentemente, il linguaggio $\mathcal{L}_0$ riconosciuto da $\mathcal{A}$) e chiede: “È $\mathcal{L}_0=\mathcal{L}$?” Il teacher risponde “sì”, in tal caso il processo di apprendimento termina

Nel caso di risposta negativa, il teacher fornisce anche un controesempio minimo $w’$ che dimostri la discrepanza, ossia un elemento di $(\mathcal{L}_0∖\mathcal{L})\cup(\mathcal{L}∖\mathcal{L}_0)$, dove $\mathcal{L}_0$ è il linguaggio ipotizzato dal learner.

Questa interazione permette al learner di aggiornare la propria ipotesi fino a quando non converge sull’automa corretto.

Perché non bastano le Membership Query da sole?

Le membership query (MQ) da sole non sono sufficienti per garantire che il learner “vinci”, ovvero che riesca a identificare completamente il linguaggio target. Ciò è dovuto al fatto che, senza un controllo globale, il learner potrebbe dover verificare un numero potenzialmente infinito di parole per essere sicuro dell’esattezza della propria ipotesi. Infatti, per i linguaggi regolari (e ancor più per quelli ω-regolari) l’insieme delle possibili parole è infinito, e controllare ogni possibile membership senza una query globale (equivalence query) sarebbe impraticabile.

Il Ruolo delle Equivalence Query

Le equivalence query (EQ) forniscono un controllo globale: quando il learner propone l’automa $\mathcal{A}$ ipotizzato, il teacher verifica se il linguaggio $\mathcal{L}(\mathcal{A})$ coincide con $\mathcal{L}$. In caso contrario, un controesempio guida il learner a correggere l’ipotesi. Anche se le EQ possono, da sole, richiedere tempo esponenziale nella verifica (per via della complessità della struttura del linguaggio), esse sono essenziali perché permettono una convergenza nel processo di apprendimento.

Black-box learning

! Nell’effettivo questo approccio permette di evitare di eseguire equivalence query perchè l’idea di base è che “se il 99% degli elementi appartiene al linguaggio reale ed è riconosciuto dal mio automa, perchè dare troppa importanza a quell’insignificante 1% che non è detto nemmeno che esista?”

Learning Strategy

Iniziamo a parlare di come fa effettivamente il learner a costruire l’automa da indovinare.

Facciamo finta di essere dei cazzo di cavernicoli con un’idea in testa e ragioniamo. I punti seguenti sono i pensieri che dovremmo fare per arrivare a una soluzione sensata per il nostro problema:

Vogliamo costruire un automa $A$, sapendo solo l’alfabeto usato, e dev’essere uguale a un automa $A’$.
Perciò per prima cosa il nostro obiettivo è quello di costruire un automa che capisca se una parola appartiene o no a un certo linguaggio.
Come facciamo a dire se una parola appartiene o no a un certo linguaggio? Semplicemente usando le nostre amate Membership Query
Quindi fondamentalmente usiamo una classe di equivalenza $\equiv_{\mathcal{L}_0}$ per raggruppare assieme tutte quelle parole che appartengono all’automa
se $u \equiv_{\mathcal{L_0}} v$ significa che $u$ e $v$ appartengono entrambe al linguaggio $\mathcal{L_0}$
Che succede se come stati dell’automa considero le classi di equivalenza indotte dalla relazione $\equiv_\mathcal{L_0}$? Bè, otterremmo un automa piuttosto banale composto da 2 stati: uno che riconosce tutte le parole della classe di equivalenza $\equiv_{\mathcal{L}0}$ e l’altro in cui finiscono le parole che non appartengono alla classe di equivalenza $\equiv\mathcal{L_0}$
però c’è un però. La relazione $\equiv_\mathcal{L_0}$ è troppo grossolana. Se due parole $u$ e $v$ appartengono entrambe a $\mathcal{L_0}$ non è detto che entrambe si comportino nella stessa maniera una volta che ci postpongo lo stesso suffisso.

Ad esempio $”ababa”$ e $”babab”$ appartengono entrambi al linguaggio $\mathcal{L} = \{ \alpha \mid \alpha = (a\cdot b)^*\cdot (a+b) + (b\cdot a)^*\cdot b\}$ ma se aggiungo $a$ ad entrambe, la prima continua ad appartenere a $\mathcal{L}$ mentre la seconda no.
vogliamo definire una relazione più precisa

Ecco quindi che entra in gioco un nome noto. Tutto si basa su lui. Proprio lui. Il vecchio, saggio, ma sempre attuale MyHill-Nerode, questa volta nella veste della relazione di equivalenza $\sim_L$.

Myhill-Nerode equivalence

L’equivalenza di Myhill-Nerode è un raffinamento della classe di equivalenza $\equiv_\mathcal{L}$ vista in precedenza (ossia usa una maglia più fine per setacciare le parole che appartengono alla stessa classe) e dice una cosa piuttosto semplice:

Due parole $u$ e $v$ appartengono alla stessa classe di equivalenza se e solo se il loro comportamento non cambia una volta che ci appiccico lo stesso suffisso

\[\text{se } u \sim_{\mathcal{L}_0} v \text{ allora } \forall t \in \Sigma^* \;\;u\cdot t \in \mathcal{L}_0 \iff v\cdot t \in \mathcal{L_0}\]

Chiaramente nel nostro caso non ci serve che le classi di equivalenza vengano verificate su tutti i possibili suffissi $\Sigma^$, possiamo relativizzarlo a un sottoinsieme $T\subseteq \Sigma^$ . Definiamo quindi la relazione $\approx_{\mathcal{L_0},T}$ come:

\[u \approx_{\mathcal{L}_0,T} v \text{ significa che } \forall t \in T \;\;u\cdot t \in \mathcal{L}_0 \iff v\cdot t \in \mathcal{L_0}\]

Vedremo come T conterrà tutti i prefissi dei minimi controesempi del linguaggio conosciuto dal teacher.

Minimalità dell’automa

Torniamo ad essere dei cazzo di cavernicoli:

vogliamo usare le classi di equivalenza per descrivere i nostri stati. Perciò se ho uno stato sono certo che tutte le parole della classe di equivalenza corrispondente si comportano alla stessa maniera una volta che ci appiccico lo stesso suffisso (quindi le transizioni vanno da una classe di equivalenza ad un’altra)
ma come rappresento una specifica classe di equivalenza? Uso uno dei suoi elementi come “soprannome” per indicare tutta la classe? Ci potrebbe stare
potrei usare una delle parole che appartiene alla classe per indicare la classe in questione, e di conseguenza con le parole che sono dentro quella classe definiscono anche un preciso stato dell’automa
come faccio però ad evitare che esistano più stati che corrispondono alla stessa classe di equivalenza?

Per rispondere a quest’ultimo quesito introduciamo il concetto di T-minimalità.

Attenzione, da qui in poi faremo riferimento agli stati dell’automa come le stringhe $s \in \Sigma^*$

Un automa è T-minimo se $\forall$ stato dell’automa $s \not = s’ $ abbiamo che $s\not\approx_{\mathcal{L_0},T} s’ $

In poche parole, un automa è T-minimo se ogni stato non appartiene alla stessa classe di equivalenza di un altro stato.

Completezza dell’automa

Allo stesso modo vogliamo garantire che per ogni possibile simbolo l’automa risponda e non si impalli. Quindi definiamo la T-completezza.

Un automa si dice T-completo se $\forall s \in S$ e $\forall a \in \Sigma$ abbiamo che $\exists s_a \in S$ tale che $sa\approx_{\mathcal{L_0},T} s_a$

Quindi in poche parole per ogni stato, per qualsiasi simbolo dell’alfabeto, esiste uno stato dell’automa in cui si finisce e per il quale la nuova stringa appartiene alla classe di equivalenza del nuovo stato (perciò non è che finisco in uno stato qualsiasi).

Ci si può aiutare a raggiungere l’idea intuitiva dietro la minimalità e la completezza guardando questa immagine:

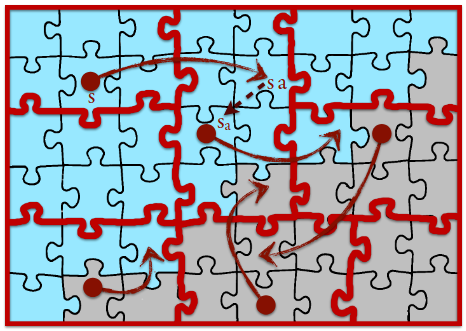
Bisogna considerare:

il quadratone come l’insieme delle parole
la parte azzurra è il linguaggio da riconoscere
i pezzi del puzzle sono classi di equivalenza
i pallini rossi sono gli stati. Non vogliamo avere più di uno stato per ogni classe, sennò non abbiamo minimalità
vogliamo che per ogni stato ci sia una transizione che porta in un altro stato o nello stesso stato se la parola creata non cambia la classe

Algoritmo

A questo punto uniamo le cose:

all’inizio non abbiamo stati, nè controesempi, quindi l’insieme S degli stati/stringhe e l’insieme T dei suffissi/controesempi sono entrambi vuoti
considero uno stato $s\in S$ (all’inizio l’unico stato che ho è quello della stringa vuota $\epsilon$) e un simbolo dell’alfabeto $a \in \Sigma$
ora voglio verificare se ci sono dei suffissi che permettono di cambiare classe di equivalenza (quindi stato), perciò controllo se per ogni suffisso $t \in T$ e per ogni stato $s’(\not = s) \in S$ ho che $\text{Membership(sat)} \neq \text{Membership(s’t)}$
se il passo precedente è vero, significa che il nuovo simbolo $a$ fa saltare in una nuova classe di equivalenza quindi aggiungo $sa$ all’insieme degli stati S
ovviamente se ogni simbolo non fa saltare in nessuna nuova classe di equivalenza significa che l’automa è T-completo

L’idea dell’algoritmo che porta alla costruzione del DFA che riconosce il linguaggio del learner è il seguente:

Inizializzazione
- Sia $S={\epsilon }$ e $T={\epsilon}$, ovvero iniziamo con solo la stringa vuota.
- $S$ rappresenta gli stati ipotetici del DFA in costruzione.
- $T$ contiene suffissi usati per distinguere gli stati.
Loop principale
- L’algoritmo termina al massimo dopo index($\sim L_0$) iterazioni, ovvero dopo aver trovato il numero minimo di stati del DFA cercato.
Verifica della T-completezza
- Un insieme S è T-completo se, per ogni stato $s$ in $S$, il suo comportamento sulle stringhe in $T$ è unico.
- Se $S$ non è T-completo, allora si aggiunge una nuova stringa a $S$, estendendolo con una nuova lettera $a$.
Costruzione del DFA candidato
- Si costruisce un DFA con:
  - Stati $S$
  - Transizioni definite da $\delta(s,a)=s_a$ (concatenazione)
  - Stato iniziale $\epsilon$
  - Stati finali determinati da $Membership(s’)$, cioè quelli che appartengono a $L_0$.
Verifica di Equivalenza
- Se il DFA costruito è corretto ($Equivalence(A)$ è vera), allora l’algoritmo restituisce il DFA.
- Altrimenti, se il DFA non è corretto, viene fornito un controesempio $w$.
Aggiornamento dell’insieme $T$
- Si aggiungono i suffissi del controesempio $w$ a $T$ per affinare la distinzione tra stati.
- Ritorna al punto 3 e ripete il processo con il DFA aggiornato.

PSEUDOCODICE:

S = T = {ε} // S is T-minimal, possibly not T-complete
loop // this will loop at most index(∼L0) times
  while S NOT T-complete
    let s ∈ S and a ∈ Σ such that
      ∀s’ ∈ S ∃t∈T Membership(s a t) ≠ Membership(s’ t)
    S = S ∪ {s a}
  A = DFA with state set S, transitions δ(s,a) = sa
  initial state ε, final states s’ s.t. Membership(s’)
  if Equivalence(A) // this surely happens
    return A // when |S| = index(∼L0)
  else
    let w be the counter-example of equivalence 
    T = T ∪ {suffixes of w} // S becomes T-incomplete and will grow at next iteration…

Matrici di Hankel

È possibile sfruttare le matrici di Hankel per avere un modo più intuitivo per applicare la procedura.

In pratica si costruisce una matrice in cui le righe sono le classi S e le colonne invece gli elementi di T.

Ciascuna cella può contenere il valore 0 o 1 a seconda che $Membership(s\cdot t)$ restituisca yes o no.

Dopodichè il procedimento è identico all’algoritmo visto in precedenza.

Se due righe sono uguali significa che lo stato è il medesimo (perchè la classe di equivalenza è la stessa).

📌 Esempio concreto di costruzione di un DFA

Supponiamo che il learner parta con: $S={\epsilon,a,b},T={\epsilon,a}$

La matrice iniziale:

H[S,T]	ε	a
ε	0	0
a	0	0
b	0	0

Il learner scopre che tutti i prefissi attuali sembrano uguali (tutte le righe sono uguali), quindi per ora assume un solo stato.

Ora il learner prova nuove parole:

Se chiede per $ab$, scopre che $H(ab,\epsilon)=1$ (perché $ab$ appartiene a L).
Aggiunge $ab$ a S e aggiorna la matrice.ab

Ora la matrice è:

H[S,T]	ε	a
ε	0	0
a	0	0
b	0	0
ab	1	0

Il learner nota che la riga di ab è diversa dalle altre, quindi introduce un nuovo stato per ab.

Ora può costruire il DFA:

Stato iniziale $q_0$ (per ε).
Stato $q_1$ per $a$.
Stato $q_2$ per $ab$ (stato finale).

Aggiunge le transizioni:

$q_0 \to_a q_1$
$q_1 \to_b q_2$ (perché abab è accettato)
$q_2$ è finale.

Alla fine, ripete il controllo con un’Equivalence Query.

Funzioni su parole

Se possiamo imparare automi, perchè non cercare di imparare funzioni? Più specificatamente funzioni monotone?

Ridefiniamo la bella relazione di Myhill-Nerode:

\[u \sim_{f_0,T} v \iff \forall t \in T\;\;\; f(ut)-f(u) = f(vt)-f(v)\]

e applichiamo essenzialmente la stessa idea applicata precedentemente.

L’approccio black-box mi permette di creare il trasduttore sequenziale che permette, dato un programma scritto in python, di calcolare il corrispettivo codice in javascript non conoscendo l’alfabeto di output?

Implicazioni del Learning Automata

Il modello di learning basato su membership ed equivalence query, inizialmente proposto per DFA (ad esempio con l’algoritmo $\mathcal{L}^*$ di Angluin), ha ispirato estensioni nel contesto degli ω-automata e delle logiche S1S/WS1S. L’idea centrale è sempre quella di avere un teacher che possiede una descrizione completa del linguaggio target e un learner che costruisce progressivamente un’ipotesi tramite feedback, anche se in questo caso il “gioco” si svolge in un ambiente in cui le proprietà $\omega$ (come la visita infinita di stati finali) devono essere verificate.

Conclusioni

Automata Learning offre un quadro in cui il learner, partendo solo dall’alfabeto, interagisce con un teacher tramite membership ed equivalence query per identificare un automa (sia per linguaggi finiti che per ω-linguaggi) che riconosca il linguaggio target.
Le membership query forniscono informazioni locali, mentre le equivalence query consentono di verificare globalmente la correttezza dell’ipotesi.
Nel dominio degli ω-linguaggi, la complessità aumenta a causa delle condizioni di accettazione (ad esempio, in automi di Büchi o Müller) e delle corrispondenti rappresentazioni logiche (S1S, WS1S), ma il modello di interazione tra teacher e learner rimane un potente strumento.
Le connessioni con omega-regolarità e le logiche S1S/WS1S garantiscono che il potere espressivo dei modelli di automi utilizzati nel learning sia sufficiente a rappresentare le proprietà temporali e infinite dei sistemi reali, come quelli modellati in verifica formale.
Infine, l’analisi comparativa tra automi di Büchi, Müller e Rabin fornisce ulteriori strumenti per affrontare problemi di learning in contesti dove il complementare, la determinizzazione e altre operazioni chiave giocano un ruolo fondamentale.