V&V-Automi a stati finiti su parole finite

Def. Deterministic Finite Automata (DFA)

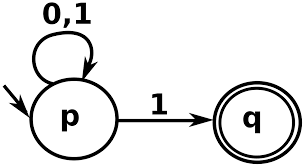
Un automa a stati finiti deterministico è un automa come questo:

Come si può vedere ci sono dei nodi, degli archi e delle label associate agli archi. Possiamo notare anche come alcuni nodi sono rappresentati da un unico cerchio, altri da due cerchi. Diamo una definizione un po’ più precisa di cosa siano i DFA: I DFA sono automi definiti dalla tupla $< \mathcal{Q}, \mathcal{F}, \delta, \Sigma, q_0 >$ dove:

• $\mathcal{Q}$ è l’insieme degli stati (i nodi)
• $\mathcal{F}$ è l’insieme degli stati finali (i nodi con doppio cerchio)
• $\delta$ è la funzione di transizione, ossia definisce come i nodi devono essere connessi tra loro dagli archi
• $q_{0}$ è lo stato di partenza (il nodo che nell’immagine riceve un arco senza label)
• $Sigma$ è l’alfabeto, ossia l’insieme dei simboli (quelle label sopra gli archi) In particolare $\delta$ è definita come una funzione del tipo

In pratica a partire da un certo stato e un certo simbolo, la funzione $\delta$ identifica il nodo di destinazione

Data una sequenza di simboli (una parola), diciamo che la parola è accettata se esiste una sequenza di transizioni che a partire dallo stato iniziale portano a uno stato finale.

Def. Non-Deterministic Finite Automata (NFA)

Gli NFA sono una variante dei DFA con la capacità del non-determinismo. A conti fatti la definizione di NFA è la stessa dei DFA, ossia una tupla $< \mathcal{Q}, \mathcal{F}, \delta, \Sigma, q_0 >$. Quello che cambia è che la funzione $\delta$ non è esattamente una funzione, ma più una relazione. Difatti mappa le coppie $(q,s)$ in più coppie $(q_{i}, s_{i})$.

L’accettazione di una parola è stabilità dall’esistenza o meno di una catena di transizioni che a partire dal stato iniziale portano a uno stato finale.
Se ogni parola di un linguaggio è accettata dall’NFA, il linguaggio si dice accettato da tale NFA.

Def. $\epsilon$-NFA

Non sto tanto a parlare di questo tipo di automa. Basta sapere che è identico agli NFA, cambia solo che l’alfabeto $\Sigma$ è esteso per contenere anche il simbolo $\epsilon$, ossia la il simbolo vuoto. Questo significa che una transizione potrebbe essere attivata anche dalla presenza di un simbolo vuoto (che ovviamente è sempre presente, quindi la transizione è sempre attiva).

Teorema di equivalenza tra NFA e DFA

Un risultato chiave è quello che consente di legare gli NFA ai DFA, in particolare stabilendo che gli NFA sono equivalenti ai DFA. Ovviamente posso trasformare un DFA in un NFA, ma come posso fare a trasformare gli NFA in DFA?

Per dimostrare questa cosa è sufficiente osservare come sia possibile, a partire da un NFA, creare un DFA che abbia

• come stati tutti i possibili sottoinsiemi di Q
• come archi le transizioni che mediante un certo simbolo “s” portano a tutti gli stati rappresentati dal nodo

Si può dimostrare per induzione sulla dimensione della parola di input come questo metodo sia efficace.

Teorema di equivalenza tra $\epsilon$-NFA e NFA

Anche in questo caso si tratta di dimostrare che a partire da un $\epsilon$-NFA si può arrivare a una rappresentazione NFA.

(McNaughton & Yamada, 1960) Teorema di equivalenza tra DFA e linguaggi regolari

Il teorema afferma che se ho un DFA posso ricavare un linguaggio regolare (ristretto) che lo rappresenta, e posso fare anche il viceversa.

Per dimostrare questo teorema ho quindi bisogno di dimostrare che

1. sono in grado di costruire un’espressione regolare a partire da qualsiasi tipo di DFA
2. sono in grado di costruire un $\epsilon$-NFA a partire da qualsiasi tipo di espressione regolare

Dimostrazione punto 1

Per dimostrare il primo punto l’idea è associare a ogni stato $q_i$ una variabile $X_i$ e costruire un sistema di equazioni a partire dall’automa $M={Q, \Sigma, \delta, q_0, F}$. Calcolando le soluzioni otterremo un’espressione regolare per ogni variabile $X_i$. Se l’insieme degli stati finali è $F={q_{j_{1}},\dots, q_{j_{n}}}$ allora per ogni variabile $X_{j_{1}}\dots X_{j_{n}}$ avremo un’espressione regolare $r_{j_{k}}$ e la concatenazione di tutte queste espressioni regolari sarà proprio la soluzione del nostro sistema di equazioni, ossia la formula che rappresenta il DFA di partenza.

Sarebbe bello se fosse così semplice, ma se fossimo catapultati nel 1000 d.C. non saprei dimostrare questa cosa semplicemente da queste poche nozioni. Quindi dobbiamo dare un po’ più di dettagli.

Consideriamo

• l’insieme ${q_{i_{1}},\dots, q_{i_{n}}}$ di stati tali che esiste un simbolo $a\in\Sigma$ per cui $\delta(q_{i_{j}},a)=q_{i}$
• l’insieme ${b_{i_{1}},\dots, b_{i_{k}}}$ di simboli tali che $\delta(q_{i}, b_{i_{j}})=q_{i}$ e mettiamo a sistema delle equazioni nella forma \(X_{i} = (X_{i_{1}}a_{i_{1}}+ \dots +X_{i_{n}}a_{i_{n}})\cdot(b_{i_{1}}+\dots+b_{i_{k}})\) dopo di che risolviamo il sistema di equazioni usando il metodo di sostituzione e ricordando che se dovessimo ottenere un’equazione del tipo $X_i = X_{i}s_{1}+s_{2}$ questa è uguale a $X_{i} = s_{2}s_{1}^*$

Dimostrazione punto 2

La dimostrazione del secondo punto è ancora più semplice. È sufficiente trovare un automa per ogni pezzetto della nostra espressione regolare. È come se avessimo un robot dei Power Rangers e dovessimo fonderli assieme per fargli fare cose più potenti. Dunque:

• per riconoscere una stringa vuota mi basta un automa tipo questo

• Per riconoscere un linguaggio vuoto mi basta un automa come quello sopra, ma senza nessun arco tra i due stati iniziale e finale.

• Per riconoscere un linguaggio ${a}$ mi serve un automa come questo.

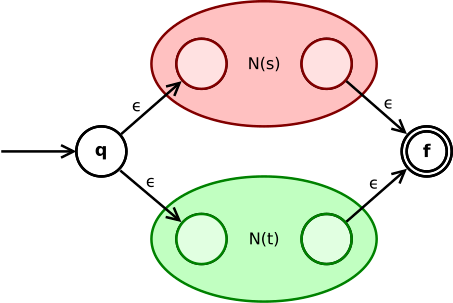
• Per riconoscere l’unione di due linguaggi mi serve un automa un po’ più complesso, con delle $\epsilon$-transizioni come questo qua.

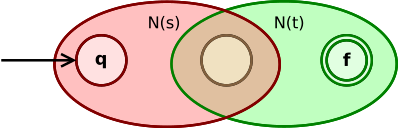
• Per riconoscere la concatenazione di due linguaggi mi serve un automa un po’ più complesso, con delle $\epsilon$-transizioni come questo qua.

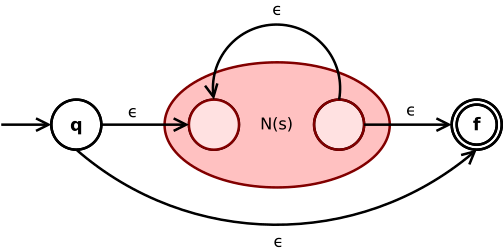
• Per riconoscere la chiusura di Kleene di un linguaggio mi serve un automa un po’ più complesso, con delle $\epsilon$-transizioni come questo qua.

Un esempio carattaristico (i veri intenditori capiranno che non ho sbagliato a digitare) si può trovare qua

Proprietà di chiusura

I linguaggi regolari sono chiusi rispetto alle operazioni di unione, concatenazione, chiusura di kleene, complementazione e intersezione. Dimostrare questa cosa è piuttosto banale. Immaginiamo di avere due linguaggi regolari $L_1$ e $L_2$

• unione -> costruisco un automa in cui lo stato iniziale porta mediante una $\epsilon$-transizione allo stato iniziale dell’automa che riconosce $L_1$ e mediante un’altra $\epsilon$-transizione allo stato iniziale dell’automa che riconosce $L_2$
• concatenazione -> costruisco un automa in cui ogni stato finale dell’automa che riconosce $L_1$ porta allo stato iniziale dell’automa che riconosce $L_2$
• chiusura di Kleene -> costruisco un automa in cui ogni stato finale riporta allo stato iniziale dell’automa
• complementazione -> inverto gli stati iniziali con quelli finali
• intersezione -> mi basta dimostrarlo usando le leggi di de Morgan, è questione di una riga

Proprietà di decidibilità

I seguenti problemi sui linguaggi regolari sono decidibili:

• problema del vuoto: l’insieme delle stringhe accettate da un DFA $M$ con n stati è non vuoto sse accetta una stringa di lunghezza inferiore a $n$
• problema dell’infinito: l’insieme delle stringhe accettate da un DFA M con n stati è infinito sse l’automa accetta una stringa di lunghezza $n<l<2n$
• problema dell’equivalenza: stabilire se i linguaggi accettati da due diversi DFA sono equivalenti
• problema dell’inclusione: stabilire se due linguaggi regolari sono in una relazione di inclusione tra loro

Dimostrazione decidibilità del problema del vuoto

-> se l’insieme delle stringhe accettate da un DFA $M$ con n stati è non vuoto allora $M$ accetta una stringa di lunghezza inferiore a $n$ Supponiamo che l’insieme non è vuoto. Prendiamo un qualsiasi suo elemento $s$ tale che $|s| = m$ . Se $m < n$ la nostra tesi è dimostrata. Se $m\ge n$ applichiamo il Pumping Lemma che ci dice che possiamo vedere $s = uvw$ con $|v| \ge 1$ e “spompiamo” (perchè qua gli spompinei non li facciamo) $s$ prendendo $s’ = uv^0w$ (che sappiamo per il Pumping Lemma appartenere al nostro linguaggio). Se $s’$ non è abbastanza piccolo ripetiamo lo spompamento finchè entriamo dentro $n$.

<- se $M$ accetta una stringa di lunghezza inferiore a $n$ allora l’insieme delle stringhe accettate da un DFA $M$ con n stati è non vuoto La dimostrazione è banale, se viene accettata una stringa è ovvio che l’insieme non è vuoto.

Dimostrazione decidibilità del problema dell’infinito

-> se l’insieme delle stringhe accettate da un DFA M con n stati è infinito allora l’automa accetta una stringa di lunghezza $n<l<2n$ L’idea è applicare nuovamente il Pumping Lemma. Se l’insieme è infinito posso considerare una stringa $z$ tale che $|z| = m > 2n$. Per il Pumping Lemma $z = uvw$ e $|uw|\ge n$ . Posso applicare uno spompamento della stringa z considerando $z’ = uv^0w$ iterativamente finchè $z’ <2n$.

<- se l’automa accetta una stringa di lunghezza $n<l<2n$ allora l’insieme delle stringhe accettate da un DFA M con n stati è infinito È ovvio che sia così. Se l’automa accetta una stringa di lunghezza $>n$ significa che c’è un ciclo nel nostro automa, perchè per il problema della piccionaia, avremo che almeno uno degli stati dell’automa è raggiunto da più di un simbolo della nostra stringa.

Dimostrazione decidibilità del problema dell’equivalenza

Possibili domande:

1. Enuncia tutte le proprietà di chiusura dei linguaggi regolari
2. Enuncia tutti i problemi di decidibilità dei linguaggi regolari
3. Dimostra che i linguaggi regolari e gli $\epsilon$-NFA hanno lo stesso potere espressivo