Information Theory - Lecture 4
Riprendiamo il teorema dell’ultima volta, ossia il [[2024-12-26-Information Theory Lecture 3#1° Shannon Theorem (Source Code Theorem)|1° teorema di Shannon]] e anche la definizione di [[2024-12-26-Information Theory Lecture 3#Definition of EL|EL]].
È possibile raggiungere la condizione per cui $EL(\varphi)= H_{D}(P) \;?$ Ossia, è possibile che la lunghezza media delle stringhe del codice sia uguale all’entropia di $P$ ?
Ad esempio: \(\begin{aligned} &A = \{a,b\}\\ &B = \{0,1\}\\ &P \neq \left\{ \frac{1}{2}, \frac{1}{2} \right\}\\ &P = \left\{ \frac{2}{3}, \frac{1}{3} \right\} \\ &H(P) <1\\ &EL(\varphi) \ge 1\\ &\varphi(a) = 0 \\ &\varphi(b) = 1 \\ &EL(\varphi) = \frac{2}{3}\cdot 1 +\frac{1}{3}\cdot{1} = 1\\ &\text{Ma allora H(P) non è raggiungibile} \end{aligned}\)
Shannon Code
L’idea è quella di assegnare un encoding di lunghezza maggiore ai simboli che hanno minor probabilità di comparire all’interno di una stringa. Per questa ragione si considera come lunghezza di encoding il negativo del logaritmo della probabilità del carattere.
Intuitivamente, se ho un vocabolario corrispondente alle parole italiane saprò che le lettere più frequenti sono ${a,e,i,o,u}$ , quindi cercherò di minimizzare il numero di caratteri necessari a codificare tali simboli. Al contrario simboli come ${k,j,w,y}$ sono molto meno frequenti e perciò mi aspetto che l’efficienza dell’encoding non abbia grosse perdite se codifico tali caratteri usando un numero più grande di simboli dell’alfabeto di output.
\[\begin{aligned} EL(\varphi) &= \sum_{i=1}^k p_{i}\cdot l_{i}\;\;\;\;\;\;\;\; l_{i}=|\varphi(a_{i})|\\ H_{D}(P) &= \sum_{i=1}^k p_{i}\cdot (-\log_{D}p_{i}) \\ \\ l_{i} &\cong -\log_{D}p_{i} \\ \\ l_{i} &= \lceil -\log_{D}p_{i} \rceil = -\log_{D}p_{i} + \beta_{i} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{ con } 0\le\beta_{i}<1 \end{aligned}\]Usando il [[2024-12-26-Information Theory Lecture 3#Theorem Direct|direct theorem]]
Se $\sum_{i=1}^k D^{-l_{i}} \le 1$
allora esiste un prefix code con lunghezze $l_i$ definibile usando una strategia greedy su un albero D-ario
Se $\beta_{i}=0$ significa che la lunghezza di encoding è identica alla lunghezza di encoding ottimale, perciò ci troviamo nel caso migliore, mentre se $\beta_{i}=1$ ci troviamo nel caso peggiore perchè significa che l’encoding del simbolo $i$ è più lungo del necessario.
Esempio:
\[\begin{aligned} &A = \{a,b\} \\ &B = \{0,1\} \\ &P = \left\{ 1-\frac{1}{32}, \frac{1}{32} \right\} \\\\ &-\log_{2}\left( 1-\frac{1}{32} \right) < 1 \to 1 \\ &-\frac{\log_{2}1}{32} = 5 \to 5 \end{aligned}\]
Shannon Encoding
\[\begin{aligned} EL(S) &= \sum_{i=1}^k p_{i}\cdot(-\log_{D}p_{i} + \beta_{i}) \\ &= \sum_{i=1}^k p_{i}\cdot(-\log_{D}p_{i}) + \sum_{i=1}^k (p_{i}\cdot\beta_{i}) \\ &= H_{D}(P) + \sum_{i=1}^k p_{i} \beta_{i} < H_{D}(P)+1 \\ \end{aligned}\] \[H_{D}(P) \le EL(S) < H_{D}(P)+1 \;\;\;\;\;\;\;\; \text{(sub-optimum)}\]Shannon-Fano Encoding
$B = {0,1}$
Split $A$ trying to have $\frac{1}{2}$ probability in each
 Ordino le probabilità e dividere quando la somma arriva a $\frac{1}{2}$
Ordino le probabilità e dividere quando la somma arriva a $\frac{1}{2}$
Esempio:
\[\begin{aligned} A &= \{a,b,c,d,e,f\} \\ B &= \{0,1\} \\ P &= \left\{ \frac{40}{100}, \frac{18}{100}, \frac{15}{100}, \frac{13}{100}, \frac{10}{100}, \frac{4}{100} \right\} \\ \end{aligned}\]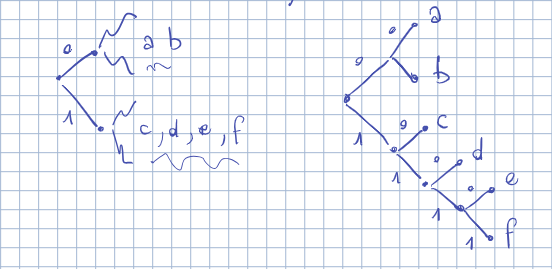
Be careful Sub-Set-Sum problem is NP-complete
\[H_{D}(P) \le EL(SF) < H_{D}(P)+1\]Cosa succede quando dobbiamo codificare tuple di n caratteri?
\[H(X\land Y) = H(X) + H(Y)\]Huffman Code
L’idea è quella di giocare sulle probabilità associate agli elementi dell’alfabeto primario. Praticamente:
- Prendo l’elemento con probabilità maggiore e gli assegno un valore (0 o 1)
- Prendo il secondo elemento con probabilità maggiore tra i rimanenti e gli assegno un altro valore (0,1)
- Se la prob del secondo elemento non è $\geq$ a quella del primo e se non è l’unico elemento rimanente, pesco il terzo elemento con probabilità più grande e gli assegno il simbolo opposto a quello precedente, dopodichè sommo le due probabilità e ripeto dal passo 2.
Alla fine dovrei ottenere qualcosa come quella dell’esempio linkato. [[Nota 8 ott 2020.pdf#page=8|Example]]
LZ77 Algorithm